
8.8 ARİTMETİK İŞLEM DEVRELERİ
8.8.1 Tanım
Toplama, çıkarma, çarpma ve bölme gibi aritmetik işlemleri yapan sayısal devrelere
aritmetik devreler adı verilir. Sayısal sistemlerde temel aritmetik işlemler toplama ve çıkarma işlemidir. Çarpma işlemi tekrarlanan toplama, bölme işlemi ise tekrarlanan çıkarma işlemi ile tanımlanır. Toplama devreleri bir çok elektronik uygulamasında da kullanılmaktadır ve aritmetik ünitelerde hız belirleyici unsurdur.
8.8.2 Toplayıcı
Devreler (Adders)
Sayısal devreler için toplama işlemini gerçekleştiren devrelere toplayıcılar (adders)
adı verilir. Toplama devreleri bir çok elektronik uygulamada da kullanılmaktadır
ve aritmetik ünitelerde hız belirleyici unsurdur. Toplama devrelerinde üç temel
faktör; devrenin hızı, kapladığı alan ve harcadığı güçtür. Aşağıda Binary
(ikilik) sayıların toplamına ilişkin temel kurallar verilmiştir.
Tablo 8.39 Binary (ikilik) sayıların toplamına ilişkin temel kurallar
İşlem |
Elde |
Sonuç |
0+0 |
0 |
0 |
0+1 |
0 |
1 |
1+0 |
0 |
1 |
1+1 |
1 |
0 |
Not : Toplama işlemi sonunda oluşan eldenin işlem sonucunun en yüksek değerlikli basamağı olduğu unutulmamalıdır.
İlk üç işlemde tek basamaklı bir sayı elde edilirken, son işlemde ikinci basamak ortaya çıkar
ve ikinci basamak
‘elde biti’
(carry bit) olarak isimlendirilir. İki biti toplayan devreler
‘yarım toplayıcı’ olarak, elde değerini temsil eden biti üçüncü bit olarak değerlendirilen ve üç bitin toplamını yapan devreler ise ‘tam toplayıcı’
olarak isimlendirilir. Yarım toplayıcı terimi, tam toplayıcıyı oluşturmak için
iki tane yarım toplayıcı kullanılmasından ileri gelmektedir.
8.8.2.1 Yarım toplayıcı (half adder)
Bir bitlik iki veriyi toplayan devrelere yarım toplayıcı (half adder) adı verilir. Bir yarım toplayıcının birer bitlik iki veri girişi için iki giriş, toplam ve oluşan eldenin gösterimi için iki tane çıkışı vardır. Toplama devrelerinde hız optimizasyonu için en temel faktör elde oluşumudur. Oluşan
elde mümkün olduğu kadar kısa sürede çıkışa ulaşmalıdır.
Toplama devrelerinin en temel elemanı, yarım toplayıcıdır. Bu devre, ikilik tabanında verilen iki tek bitlik sayıyı toplamaktadır. Yarım toplayıcı devresi tek başına çok faydalı olmasa da, daha büyük toplama devrelerinin alt bloğu olarak kullanılır. Devrenin çalışma şeklini daha iyi anlamak için ikilik tabanda toplama kurallarını göz önüne alalım;
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0
burada aşağıda ayrıntılı olarak anlatılacağı gibi Carry (elde) kullanılacaktır. 1 + 1 = 0 olurken Carry ise 1 olacaktır.
Aşağıda bir yarım toplayıcının tasarımı anlatılmıştır;
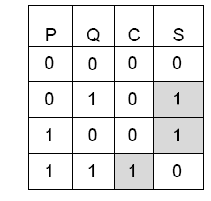
Bir bitlik iki veriyi P ve Q ile adlandırarak tasarlanacak devrenin, iki binary sayının toplanması işlemini gerçekleştirmesi istenir. Toplama işleminin gösterimi için sonuç (Sum -S ) ve elde (Carry - C) olmak üzere iki tane çıkış olması gerekir.
 |
 |
|
|
Şekil 8.75 Doğruluk tablosundan S ve C fonksiyonlarını yazma |
Not: Çıkışlara ait Lojik ifadeyi elde ederken her bir çıkışa ait olan minimum terimin yazıldığı görülmelidir.
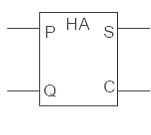
Örnek 8.31 Aşağıda bir yarım toplayıcının (Half Adder) Lojik diyagramı ve sembolü verilmiştir.
 |
|
Şekil 8.76 Yarım toplayıcı blok şeması |
8.8.2.2 Tam toplayıcı (full adder)
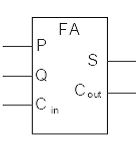
İkinci temel toplayıcı devrelere tam toplayıcı (full adder) adı verilir. Tam toplayıcı iki adet yarım toplayıcının bir OR kapısıyla birleşimi neticesinde elde edilir.Üç bitlik verilerin toplanması işlemini gerçekleştiren devrelerdir. Devrenin toplama işlemi için üç giriş, sonucun gösterimi için iki tane çıkışı vardır. Girişlerden ikisi toplama işleminin yapılacağı iki veriyi gösterirken; diğer giriş düşük değerlikli basamaktan oluşan elde girişi içindir. Aşağıda bir tam toplayıcının doğruluk tablosu verilmiştir;
|
|
|
|
Şekil 8.77 Doğruluk tablosundan S ve C fonksiyonlarını yazma |
Örnek 8.32 Aşağıda bir tam toplayıcının lojik diyagramı ve sembolü verilmiştir.
 |
|
Şekil 8.78 Tam toplayıcı blok şeması |
8.8.2.2.1 Tam toplayıcı devresinin karnaugh haritası yöntemiyle tasarlanması
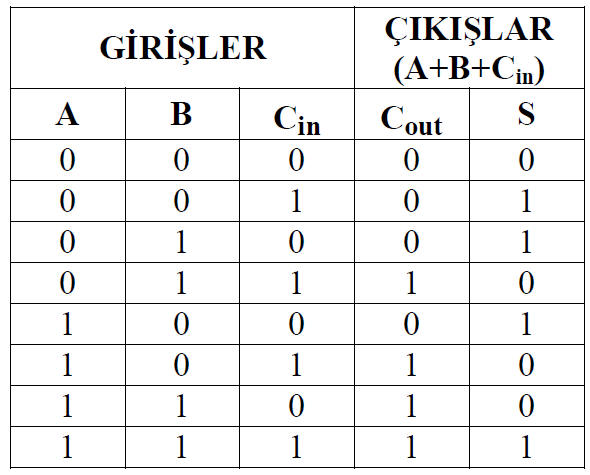 |
S = A'B'Cin + A'BCin' + AB'Cin' + ABCin Cout = A'BCin + AB'Cin + ABCin' + ABCin
|
|
Şekil 8.79 Doğruluk tablosu ve çıkış fonksiyonları |
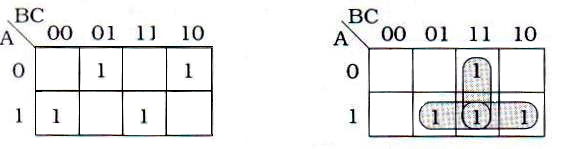
Toplayıcı tasarımında, doğruluk tablosunda giriş değişkenlerinin alabileceği değerler sıralandıktan sonra, kombinasyonlarda bulunan birlerin değerleri Boolean kurallarına göre toplanıp, sonuçlar S ve Cout kolonlarına yazılır. Devrede iki çıkış bulunduğundan, her bir çıkış için uygun olan değerleri içeren sütunlar oluşturulur ve sütunlardaki değerler Karnaugh haritalarına taşınır. Karnaugh haritalarından lojik eşitlikler elde edilir ve elde edilen eşitliklerin lojik şemaları çizilir.
 |
|
Şekil 8.80 Karnaugh haritası |
Cout = AC + AB + BC
S = AB'C' + A'B'C + A'BC' + ABC
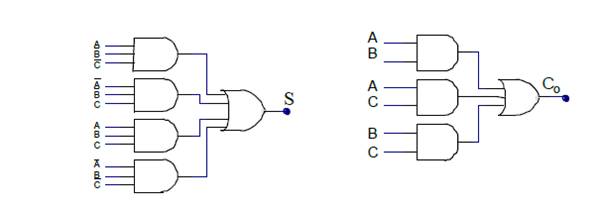
Şekil 8.79’deki doğruluk tablosundaki değerlerin Karnaugh haritalarına taşınması ile Şekil 8.80’deki haritalar elde edilir. Haritalardan elde edilen S ve Cout eşitliklerine ait devrelerin çizilmesi ile, Şekil 8.81’daki lojik devreler oluşur.
 |
|
Şekil 8.81 Tam toplayıcı lojik devresi |
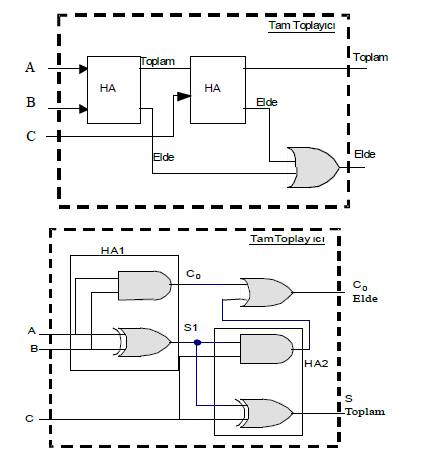
Tasarım sonucunda çizilen lojik devrelerle yapılabilecek tam toplama işlemi, iki adet yarım toplayıcı ve bir VEYA kapısı kullanılarak gerçekleştirilebilir. Bu şekilde gerçekleştirilen devrede; ikinci yarım toplayıcının S çıkışı, ilk yarım toplayıcının S çıkışı ile C nin Özel-VEYA ya uygulanmasının sonucudur.
 |
|
Şekil 8.82 İki yarım toplayıcı ve VEYA kapısı ile tam toplayıcı elde edilmesi |
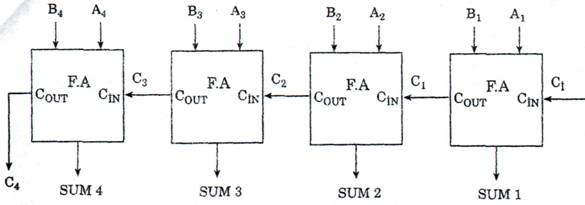
8.8.2.3 Paralel toplayıcı devreler
n bitlik iki binary sayıyı toplayan devreye paralel toplayıcı denir. Paralel toplayıcı devresinde n sayıda tam toplayıcı devresi kullanılır. Devreye A ve B binary sayılarının tüm bitleri aynı anda uygulanır. Tam toplayıcıdan gelen çıkış eldesi, bir sonraki (solundaki) tam toplayıcının giriş eldesine bağlanır. n bitlik paralel toplayıcılar, MSI entegrelerine bir örnektir. Paralel
toplayıcılarda, full adderlar(tam toplayıcı) paket olarak gösterilir. Aşağıdaki şekillerimizde 4 bitlik iki binary sayıyı toplayabilen paralel toplayıcı devresi gösterilmektedir. Ci, paralel toplayıcının giriş eldesini, C4 ise çıkış eldelerini gösterir. SUM1, SUM2, SUM3 ve SUM4 çıkışları toplam bitleri gösterir. Örnek olarak 7483 IC tipi TTL entegreleri gösterilebilir.
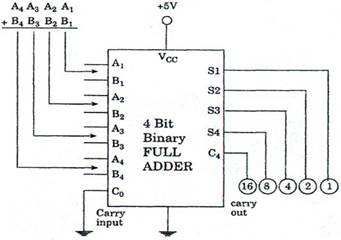 |
| Şekil 8.83 7483 Entegresiyle yapılan toplayıcı devresi |
 |
|
Şekil 8.84 4 Bitlik paralel toplayıcı devresi |
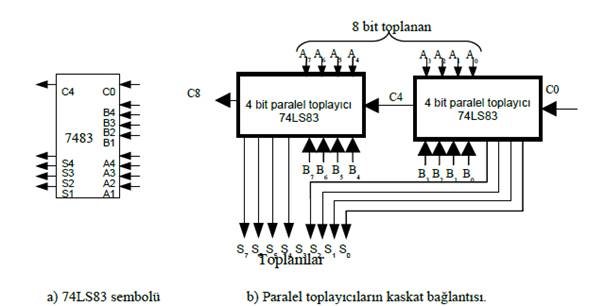
Yapılan örnekte, dört bitlik iki sayının toplanması açıklandı. Günümüz bilgisayar sistemlerinde aynı anda toplanacak sayılar 8 ile 64 bit arasında değişmektedir. Pratikte tüm FA'lardaki toplama işlemi aynı anda yapıldığından, paralel toplayıcılar çok hızlı işlem yaparlar. Piyasada 7483, 74283, 74LS83A ve 74HC283 (CMOS) gibi farklı yapıda dört bitlik paralel toplayıcılar bulunmaktadır. Şekil 8.81.a'da 74LS283 tipi dört bitlik paralel toplayıcının fonksiyon şeması görülmektedir. Dört bitlik paralel toplayıcı iki adet dört bitlik girişe (A3, A2, A1, A0 ve B3, B2, B1, B0) ve en düşük basamaklı bit (LSB) için kullanılan Co girişine sahiptir. Çıkış olarak; dört adet toplam çıkışı (S3, S2, S1, S0) ile birlikte en yüksek basamaklı bitin elde çıkışı olan C4 bulunur.
 |
|
Şekil 8.85 Toplayıcı sembolü ve paralel toplayıcıların kaskatı bağlanması |
Paralel toplayıcıları kaskat bağlayarak, daha fazla sayıdaki bitleri paralel olarak toplamak mümkündür. Şekil 8.81.b'de iki adet dört bitlik paralel toplayıcının blok şeması görülmektedir. Kaskat bağlanan paralel toplayıcılarda, sağdaki toplayıcı düşük basamak değerlikli dört biti toplayarak, bitlerin toplamını ve toplam sonucunda oluşan elde bitini çıkış olarak verir. Yüksek değerlikli bitleri toplayan ikinci paralel toplayıcı, elde girişi olarak sağdaki toplayıcıdan elde edilen C4 çıkışını kullanır ve bitlerin toplamı ile elde bilgisini çıkış olarak verir. C8 çıkışı, ikinci paralel toplayıcının işlemler sonucunda elde ettiği elde değerini gösterir. Bu çıkış elde bilgisi olarak daha sonraki toplayıcılar için kullanılabilir.
Örnek 8.33 1001 ve 1010 sayılarını toplayabilen paralel toplayıcı devresini çiziniz ve işlemi devre üzerinde yapınız.
Verilen iki binary sayı 4 bitlik olduğu için, paralel toplayıcıda 4 adet paket (Full Adder) kullanılmalıdır. Verilen örnekte A = 1001 ve B = 1010 olarak verilmiştir.
A4 A3 A2 A1
1 0 0 1
B4 B3 B2 B1
1 0 1 0
 |
|
Şekil 8.86 4 Bitlik paralel toplayıcı |
Sadece işaretli sayılar ile yapılan işlemler sonucunda oluşur. Taşma oluşması, elde edilen sonucun ayrılmış olan bit sayısı ile gösterilemediğini belirtir. İşleme girilen sayılar ile elde edilen sonucun işaretleri arasında aşağıdaki ilişki varsa taşma oluşmuş demektir.
8.8.3.1 Toplayıcı devrelerde taşma durumu
Toplama/ çıkarma zamanı en büyük değerli basamaktan elde alınması ya da dışarıya elde verilmesi durumunda taşma olayı gerçekleşebilir. Bu durum işlemin sonucunun yanlış çıkmasına neden olur (yani pozitif olması gereken bir sonuç negatif çıkabilir). Elle yapılan işlemlerde taşma sorun olmaz fakat sayısal bilgisayarlarda sorun olur. Çünkü kaydediciler sınırlıdır. Kaydedicinin uzunluğu n bitlik ise bunun içine (n+1) bit yerleştirilememektedir. Bundan dolayı bir çok işlemci taşma olayının olup olmadığına bakar, eğer olursa bir taşma flip-flobu devreye girer.Taşma farklı işaretli sayılarda meydana gelmez, aynı işaretli sayılarda meydana gelir. Sayının biri pozitif diğeri negatif olduğunda taşma olmaz, sonuç daima mutlak değerce büyük sayıdan daha küçüktür. Her iki sayı pozitif ya da her iki sayı negatif olduğunda taşma olur.
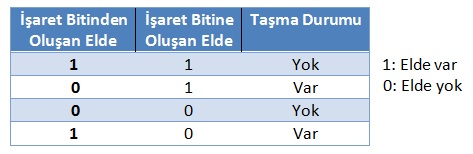
Taşmanın belirlenmesi kuralı;
1) Eğer toplama esnasında toplamın büyük bitinde ve işaret bitinde elde oluşmuşsa taşma yoktur,
2) Eğer toplama esnasında toplamın büyük bitinde elde oluşmuş; işaret bitinde elde oluşmamışsa taşma vardır,
3) Eğer toplama esnasında toplamın işaret bitinde ve büyük bitinde de elde oluşmamışsa taşma yoktur,
4) Eğer toplama esnasında toplamın büyük bitinde elde oluşmamış; işaret bitinde elde oluşmuşsa taşma vardır.
Bunu aşağıdaki tablo ile gösterecek olursak;
Yazmış olduğumuz kuralı örneklerle gösterelim:
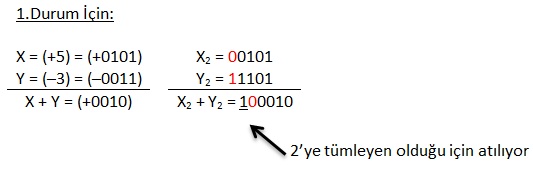
Bu örnekte sayının hem büyük bitinde hem de işaret bitinde elde oluştuğu için taşma yoktur.

Çözmüş olduğumuz örnekte görüldüğü üzere sayının büyük bitinde elde oluşmuş; işaret bitinde ise elde oluşmamıştır. Sonuç pozitif olması gerekirken negatif bir değer elde edilmiştir. (Negatif taşma var.)
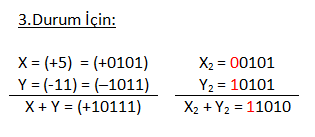
Bu örnekte işaret ve büyük bitte elde oluşmadığı için taşma yoktur.
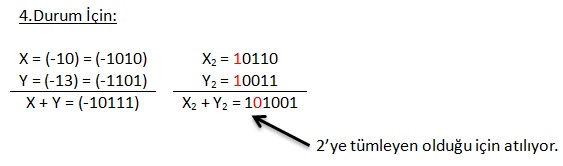
Çözmüş olduğumuz bu örnekte de görüldüğü üzere sayının büyük bitinde elde oluşmamış; işaret bitinde ise elde oluşmuştur. Sonuç negatif olması gerekirken pozitif bir değer elde edilmiştir. (Pozitif taşma var.)
Taşmayı, toplama süreci bittikten sonra da belirlemek mümkündür. X ve Y toplananların işaret bitleri değerleri, Z ise toplamın işaret bit değeri olmak üzere; bunun için aşağıdaki hesaplama kullanılabilir:
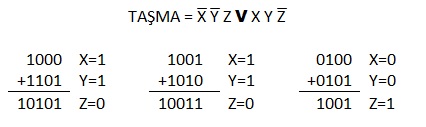
Yukarıda vermiş olduğumuz formüle çözmüş olduğumuz örneklerin işaret bitlerinin değerleri koyularak taşmanın olduğu kolaylıkla görülebilir:
1. Örnek için; Taşma=0*0*1 V 1*1*1 =1 (taşma var)
2. Örnek için; Taşma=0*0*1 V 1*1*1 =1 (taşma var)
3. Örnek için; Taşma=1*1*0 V 0*0*0 =0 (taşma yok)
8.8.3.2 Çıkarıcı devrelerde taşma durumu
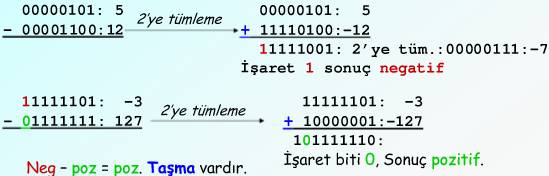
Toplama da olduğu gibi işaretli sayıların çıkarılmasında da taşma olabilir. Çıkarmada iki durumda taşma oluşabilir ;
poz - neg => neg ve neg - poz => poz
Örneğin ;
8 bitlik işaretli sayılar ile çıkarma
8.8.4 Çıkarıcı Devreler (Subtractor)
Lojik devrelerde yapılan ikinci temel işlem çıkarmadır. İki bitin çıkarılmasını yapan devreye
yarım çıkarıcı, üç bitin çıkarılmasını yapan devreye
tam çıkarıcı devresi denir.
8.8.4.1 Yarım çıkarıcı devresi (Half subtractor)
İki bitin çıkarması işlemini yapan çıkarıcı devresinde, iki giriş ve iki çıkış bulunur. Çıkışlardan birisi sayının farkını, diğeri borç bitini gösterir. İki bitin çıkarılması işleminde dört farklı durum oluşur.
|
Tablo 8.40 Yarım çıkarıcı |
|
A,B: Girişler Bout: Borç D: Fark D = |
Doğruluk tablosu incelendiğinde borç çıkışının A < B durumunda ‘1’ olduğu görülür. Yani B sayısı büyüktür ve A' dan çıkarılmak isteniyor. B sayısı A' dan bu durumda çıkarılamayacağı için A sayısına borç olarak bir solundaki haneden borç verilir. Taban 2 olduğu için bir üst basamaktan alınan sayı bir sağ basamağa 2 olarak geçer. 2' den 1 çıkınca fark ‘1’ olur. Dolayısıyla borç da ‘1’ olur.
 |
8.8.4.2 Tam çıkarıcı devreler (Full subtractor)
Daha düşük değerli basamak tarafından ‘1’ borç alınmış olabileceğini dikkate alarak iki biti birbirinden çıkaran bileşik devre
tam çıkarıcı olarak isimlendirilir. 3 giriş ve 2 çıkışa sahip tam çıkarıcı devresinde girişler;
çıkarılan, çıkan ve borcu gösterirken, çıkışlardan biri farklı diğeri borcu gösterir.
|
Tablo 8.41 Doğruluk Tablosu |
GİRİŞLER |
ÇIKIŞLAR |
|||
A |
B |
C |
Fark |
Borç |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
Şekil 8.87 Karnaugh haritası |
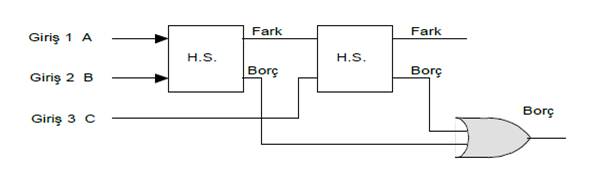
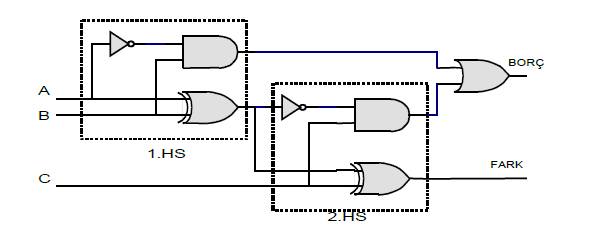
8.8.4.2.1 İki yarım çıkarıcı kullanılarak tam çıkarıcı elde edilmesi
İki yarım toplayıcı kullanılarak tam toplayıcı yapıldığı gibi, iki yarım çıkarıcı (H.S.)
kullanılarak tam çıkarıcı oluşturulabilir. İki yarım çıkarıcı ile oluşturulan tam çıkarıcı devresinde, I. Yarım çıkarıcının ‘Fark’ çıkışı II. yarım çıkarıcının girişlerinden birisi
olarak uygulanırken, C girişi ikinci yarım çıkarıcının diğer girişine uygulanır. İki yarım çıkarıcının ‘Borç’ çıkışları bir ‘VEYA’ kapısı ile birleştirilerek, tam çıkarıcı devresi ‘Borç’ çıkışı elde edilir.
Şekil 8.88'de blok şeması görülen tam çıkarıcı devresinde blok olarak gösterilen yarım çıkarıcıların yerine acık devrelerinin yerleştirilmesi ile tam toplayıcı lojik devresi elde edilir
(Şekil 8.88).
 |
 |
|
Şekil 8.88 İki yarım çıkarıcı ile tam toplayıcı oluşturulması blok şeması |
 |
|
Şekil 8.89 Paralel çıkarıcı devresinin blok diyagramı |
Blok diyagramdaki borç çıkışı "1" ise çıkarmanın sonucu pozitif, "0" ise negatif olur.
4 bitlik toplama işleminin gerçekleştirildiği 7483 entegresi ile aynı zamanda 4 bitlik çıkarma işlemi de gerçekleştirilir.
C0 = 0 olduğu zaman toplama,
C0 = 1 olduğu sürece de çıkarma işlemi yapar. A bitleri entegreye aynen uygulanırken, B bitleri de değilleri alınarak entegreye uygulanır.
8.8.5 İki Tümleyeni ile Toplama ve Çıkarma İşlemi
Birçok bilgisayar sistemi, negatif sayıları ifade etmek veya çıkarma işlemini gerçekleştirmek
için ‘2 tümleyeni’ aritmetiğini kullanır. Negatif sayıları ifade etmek için 2 tümleyeni
aritmetiği kullanılıyorsa, işaretli (-veya +) sayıların toplanması ve çıkarması işlemleri
yalnızca toplama yolu ile gerçekleştirilir.
8.8.5.1 Toplama işlemi
Negatif sayıların 2 tümleyeni formunda ifade edilmesi durumunda pozitif ve negatif sayıların
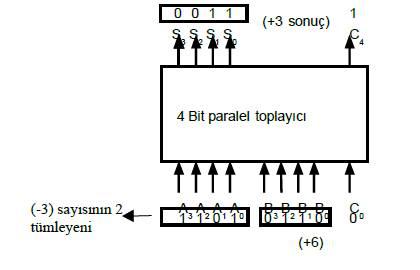
toplanması temel paralel toplama devresi ile gerçekleştirilebilir. Şekil 8.87’da (-3) ve (+6)
sayılarının paralel toplayıcı ile toplanması işlemi görülmektedir.
Yapılan işlem ‘Toplama’ olmasına rağmen, sayıların işaretleri farklı olduğundan toplanan
sayıların farkı alınır. Fark alma işleminde; ‘+’ işaretli sayıya, ‘-’ işaretli sayının iki tümleyeni eklenir.
Bulunan sonuçta elde olup olmadığına bakılır:
- Elde varsa atılır ve bulunan sonuç pozitiftir.
- Elde yoksa, elde edilen sayının ‘2 tümleyeni’ alınır ve sayının önüne ‘-’ işareti
konur.
Örnek 8.34 (-3) ve (+6) sayılarını, ikili paralel toplayıcı ile toplayalım. (-3) sayısının tümleyeni A girişlerine, pozitif (+6) sayısı ise B girişlerine uygulanırsa, fark çıkışlarından sonuç elde edilir. Borç çıkışını temsil eden C4 çıkışı ‘1’ olduğundan, sonuç pozitiftir.
 |
|
Şekil 8.90 Negatif ve pozitif sayıların paralel toplayıcı ile toplanması |
8.8.5.2 Çıkarma işlemi
Çıkarma işlemi için 2 tümleyen aritmetiği yöntemi kullanılması durumlarında,
çıkan sayının
2 tümleyeni alınarak toplama işlemi yapılır. Örneğin, A-B işlemi yapılıyorsa, A
sayısı olduğu gibi bırakılıp, B sayısının 2 tümleyeni alınır. Daha sonra, A
sayısı ile tümleyeni
alınan B sayısı toplanır ve iki sayı arasındaki fark toplayıcı çıkışından okunur.
Dört bitlik paralel toplayıcı devresi, yukarıda açıklanan yöntem ile çıkarma işlemi yapacak
şekilde düzenlenebilir. Daha önceki bölümlerden hatırlanacağı üzere, ikili
sayının 2 tümleyeni, her bir bitin tersi yazılarak ve en düşük değerlikli bite
1' ekleyerek elde edilir.
Bu işlem, B sayısının terslenmiş bitlerinin B3, B2, B1 ve B0 girişlerine,
eklenen '1' sayısının
ise C0 girişine uygulanması ile gerçekleştirilir. Böylece, B sayısındaki
rakamların tersi alınıp,
en düşük değerlikli basamağa '1' eklenmiş olur. A sayısının doğrudan A3, A2, A1 ve A0
girişlerine uygulanması ile gerekli bilgiler paralel toplayıcı girişlerine
uygulanır (Sekil 8.91). Dört bitlik paralel toplayıcıda S0 - S3
çıkışları çıkarma işleminin sonucunu gösterirken, C4
çıkışı sonucun '-' veya '+' olduğunu belirtir. C4 =1 ise sonuç pozitif, C4 = 0 ise
sonuç
negatiftir.
 |
|
Şekil 8.91 Çıkarma işleminin iki tümleyeni kullanarak paralel toplayıcılar ile gerçekleştirilmesi |
Örnek 8.35
Çıkarma işleminin nasıl yapıldığını açıklamak için; (+4) - (+6) işlemini yapalım.
1) A (+4 = 0100) ve B (+6 = 0110) sayıları toplayıcı girişlerine uygulanır. Ancak, B
sayısının 2 tümleyeni alınması gerektiğinden, B sayının 2 tümleyeni alınarak
1010 şeklinde
B girişine uygulanmalıdır.
2) Bu durumda, 0100 sayısı ile 1010 sayısı, C0=1 eklenerek toplama işlemine tabi
tutulur.
3) Sonuç olarak 1110 sayısı elde edilir. Bu sayının işaret biti olarak
0 değerine
sahip olması, sonucun negatif ve 2 tümleyeni formunda olduğunu gösterir.
4) Bulunan sayının 2 tümleyeni alınarak önüne '-' işareti konulmasıyla, doğru
sonuç (-0010) bulunur.
Aynı entegreyi toplama ve çıkarma devresi olarak kullanmak mümkündür. Bu şekilde tasarlanan devreler Flip-Flop ve kaydedici içerdiğinden daha sonraki konularda
incelenecektir.
8.8.6 Çarpma Devresi
Binary sayılarda çarpma işleminin nasıl olduğu "Binary Sayılarda Dört İşlem" konusunda işlenmişti. Aşağıdaki örneklerde çarpma işlemini gerçekleştiren lojik devrelere yer verilmiştir. Aynı zamanda çarpma işlemi tekrarlanan toplama işlemleri ile de gerçekleştirilebilir. 7485 entegresinin kaskad bağlanması ile çarpma devresi oluşturulabilir.
8.8.6.1 Çarpma devresi tasarımı ve binary çarpma devresi
Örnek 8.36 2 bitlik binary sayısının karesini alan lojik devreyi tasarlayınız.
|
Tablo 8.42 2 bitlik binary sayısının karesini alan lojik devrenin doğruluk tablosu |
| GİRİŞLER | ÇIKIŞLAR | ||||
| A | B | F3 | F2 | F1 | F0 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
Lojik devrenin iki girişi vardır. 22 = 4 değişik durumu bulunur. Önemli olan bu lojik devrenin kaç çıkış değişkeninin olmasıdır. Bunu bulmanın en basit yolu şudur: Giriş değişkenlerinin en büyüğü alınır. Bu örnekte girişin en büyük değeri decimal 3 sayısıdır (11)2. Bunun karesi olan 9 sayısı en az 4 bit olarak yazılacağından bu devrenin çıkışı 4 tanedir. Çıkış fonksiyonuna doğruluk tablosunda çıkışın her bir çıkış değişkeni için 1 olan yerlerin ifadesi yazılır.
F3 = AB
F2 = AB
F1 = 0
F0 = ÂB + AB = B(Â + A) = B
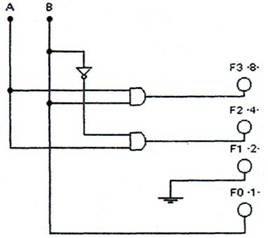 |
|
Şekil 8.92 bitlik binary sayının karesini alan lojik devre |
Bu çıkışlardan sadece F0 çıkış değişkeni sadeleştiği için, bu devrenin en sade lojik diyagramı aşağıdaki gibi olur:
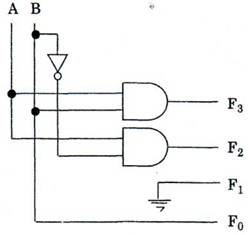 |
|
Şekil 8.93 2 bitlik binary sayının karesini alan lojik devrenin sadeleştirilmiş hali |
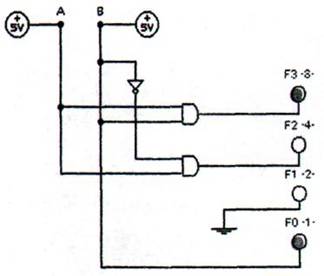 |
| Şekil 8.94 11 sayısının karesi olan 1001 sayısının elde edilmesi |
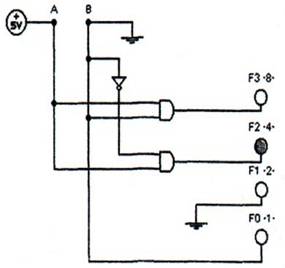 |
| Şekil 8.95 10 sayısının karesi olan 0100 sayısının elde edilmesi |
A girişine 1, B girişine 0 uygulandığında bu devre 10 sayısının karesine eşit olarak çıkışta 0100 sayısını vermiştir. Yine aynı devrenin A girişine 1, B girişine de 1 uygulandığında çıkıştan 1001 sayısı elde edilmiştir. Birinci uygulamada 2 nin karesi 4, ikinci uygulamada ise 3 sayısının karesi olan 9 sayısı elde edilmiştir.